一次IIRフィルタの簡単な実装を続けよう。以前の

の記事から、一次遅れのIIRフィルタの計算式は
$$y(nT) = x(nT) + e^{-\frac{T}{\tau}} * y((n-1)T) (式8)$$
となることが分かっている。この式を変形すると
$$y(nT) = x(nT) – (1-e^{-\frac{T}{\tau}}) * y((n-1)T) + y((n-1)T) (式9)$$
となる。
ブロック図で書くと
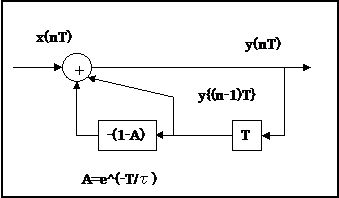
となる。
今までの記事では、係数 $1 – e^{-\frac{T}{\tau}}$ を
$$1 – e^{-\frac{T}{\tau}} = \frac{1}{16}$$
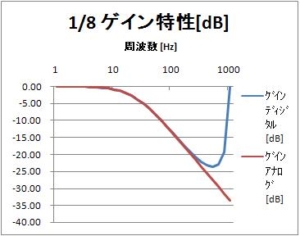
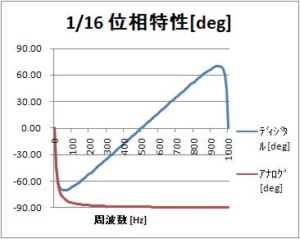
すなわち、右シフト演算4回として、実装した場合の各種波形グラフを見てきた。
ディジタルフィルタの計算式は、
$$y(nT) = x(nT) – \frac{1}{16} * y((n-1)T) + y((n-1)T) (式11)$$
である。
このとき、たとえばサンプリング周期T=1msとすると、時定数は約15msになる。
各種波形は以下の記事を参照して下さい。
- インパルス応答の時間波形(整数計算)
- ステップ応答の時間波形(整数計算)
- 正弦波入力応答の時間波形(整数計算)
- 周波数応答(リニア周波数軸、整数計算)
- 周波数応答(ログ周波数軸、整数計算)
今回は、時定数を変えてみよう。たとえばサンプリング周期T=1msのとき、時定数は約7msになるようにする。係数としては、1/16を1/8にする。右シフト3回で実装することを目論んでいる。
$$1 – e^{-\frac{T}{\tau}} = \frac{1}{8}$$
よって、ディジタルフィルタの計算式は
$$y(nT) = x(nT) – \frac{1}{8} * y((n-1)T) + y((n-1)T) (式24)$$
となる。
正確な時定数τは
$$e^{-\frac{T}{\tau}} = 1 -\frac{1}{8} = -0.875$$
にて、サンプリング周期T=1msとすれば、時定数
$$\tau = 7.488876[ms]$$
である。
さて、波形を示す。
ステップ応答の時間波形(整数計算)
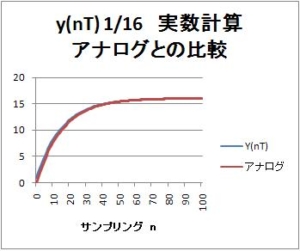
127のステップ入力の場合の応答である。時定数$\tau =7.488876$[ms]のアナログローパスフィルタの応答と比較している。横軸は、サンプリングn。サンプリング周期T=1msとすれば、横軸は時間[ms]。
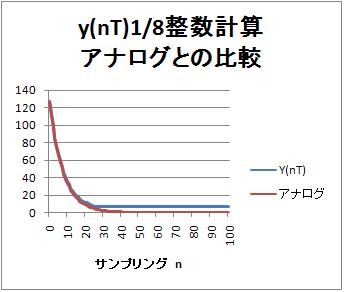
ディジタルフィルタ出力$y(nT)$の場合は、ゼロに近づかない。7で飽和する。途中の1/8で7が桁落ちでゼロになってしまい、演算結果に反映されず、残ってしまう。
ステップ応答の時間波形(整数計算)
ディジタルフィルタは127のステップ入力を入れると、最終値は$127 * 8 = 1016$になる。最終値がなぜ8倍されるかというのは、「最終値の定理」から決まる。
最終値の定理については、
を参照。
グラフでは、1016のステップ入力のアナログ1次ローパスフィルタ出力と比較している。
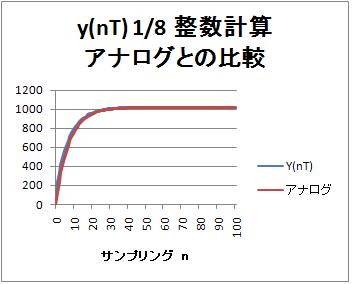
ほぼ同じになる。
エクセルデータはこちら
係数1/8の一次IIRフィルタのステップ応答、インパルス応答 Excelデータ