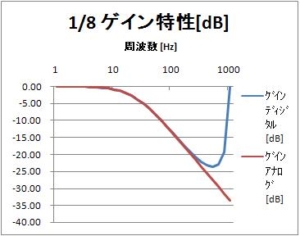
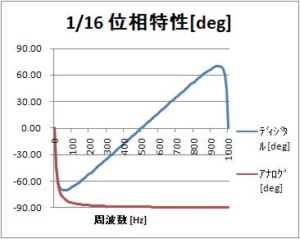
今回のミッション
超簡単な一次のIIRフィルタ
$$y(nT) = x(nT) – \frac{1}{16} * y((n-1)T) + y((n-1)T) (式11)$$
に連続したパルスを入力してみる。
計算の簡単化のために、係数1/16を使用している。サンプリング周期T=1msの場合、時定数$\tau$ は約15msになる。設計の詳細については、前の記事
あわせて読みたい

【IIRフィルタ】第1回:インパルス不変法による一次IIRフィルタ設計(基本、初歩)
さて、FIRフィルタの次は、IIRフィルタを設計してみる。 FIRフィルタに関しては【FIRフィルタ】シリーズに詳しく書いてあります。 https://primemotion.com/filter FIR...
および、係数1/16の背景については、
あわせて読みたい

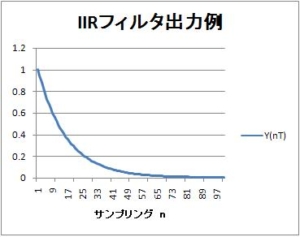
【IIRフィルタ】第3回:簡単一次IIRフィルタのインパルス応答波形
前回のおさらい 1次のIIRローパスフィルタは、以下の式で実現できる。 $$y(nT) = x(nT) - (1-e^{-\frac{T}{\tau}}) * y((n-1)T) + y((n-1)T) (式9)$$ ここで、例...
を参照してほしい。
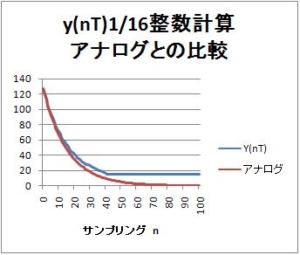
さて、整数演算のため、途中の1/16で桁落ちするので、パルスは127の大きさのパルスを入力する。横軸はサンプリングn、サンプリング周期T=1msの場合は時間[ms]になる。
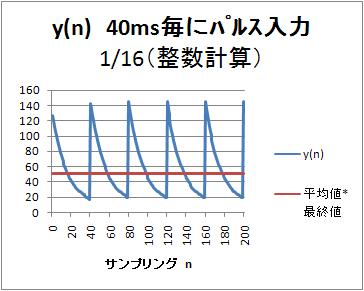
40ms周期でパルスを入力した場合の出力$y(nT)$
40ms毎に1msの127の値が入力されるので、平均値127*1ms/40msに、最終値16を掛けた値と比較している。
最終値については、こちらの記事を参照してほしい。
あわせて読みたい
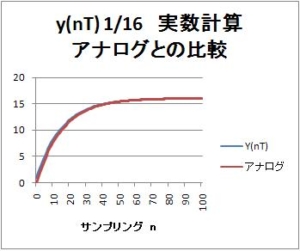

【IIRフィルタ】第4回:簡単一次IIRフィルタのステップ応答波形
前回のおさらい 1次IIRフィルタで、サンプリング周期T=1ms、時定数 $\tau$=15ms程度のローパスフィルタを実装しようとしている。 計算式はさきの記事より、 $$y(nT) = ...
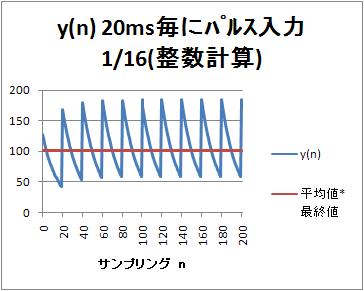
20ms周期でパルスを入力した場合の出力$y(nT)$
平均値127*1ms/20msに対して、最終値16を掛けた値と比較している。
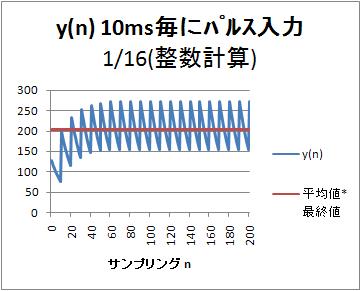
10ms周期でパルスを入力した場合の出力$y(nT)$
平均値127*1ms/10msに対して、最終値16を掛けた値と比較している。
5ms周期でパルスを入力した場合の出力$y(nT)$
平均値127*1ms/5msに対して、最終値16を掛けた値と比較している。
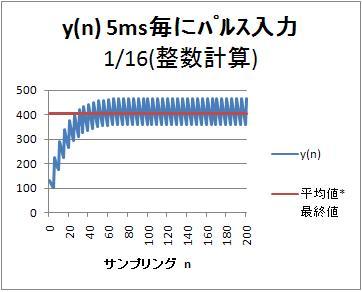
出力y(nT)は、ローパスフィルタが効いて、連続パルス入力の平均値を得ていることがわかる。読者のみなさん、使えそうですか?
エクセルのデータはこちら
簡単1次IIRフィルタに連続パルス入力入れた出力波形 Excelデータ