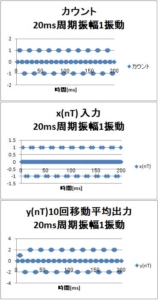
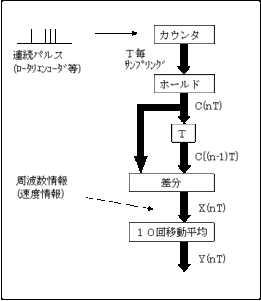
単純移動平均ゲイン特性のまとめ
先の記事の周波数特性の式から、振幅の部分を取り出して
・2回平均
$$g(\omega) = |2 * con(\frac{\omega T}{2})|$$
・4回平均
$$g(\omega) = \frac{|sin(2\omega T)|}{|sin(\omega T/2)|}$$
・8回平均
$$g(\omega) = \frac{|sin(4\omega T)|}{|sin(\omega T/2)|}$$
・10回平均
$$g(\omega) = \frac{|sin(5\omega T)|}{|sin(\omega T/2)|}$$
以上をグラフにする。サンプリング周期T=1msとしている。横軸は周波数[Hz]。
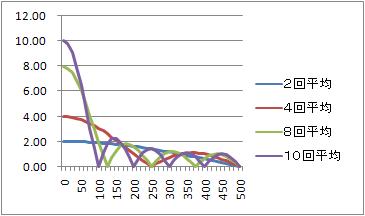
2回平均は、周波数ゼロ、すなわち、直流にて、ゲインは2となる。4回平均は、4。8回平均は、8。10回平均は10。直流でのゲインを1になるように規格化して、比較しやすくする。つまり、2回平均のゲイン特性は、2で割る。4回平均のゲイン特性は、4で割る。他も同様。
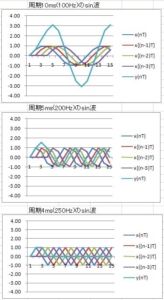
規格化したグラフは、

サンプリング周期T=1ms、すなわちサンプリング周波数は1000Hzである。このとき、
- 2回平均の場合は、サンプリング周波数の1/2の500Hzでゲインゼロ
- 4回平均の場合は、サンプリング周波数の1/4の250Hzでゲインゼロ
- 8回平均の場合は、サンプリング周波数の1/8の125Hzでゲインゼロ
- 10回平均の場合は、サンプリング周波数の1/10の100Hzでゲインゼロ
となる。
例えば、他のサンプリング周波数で、2000Hzにしたら、同様に
- 2回平均の場合は、サンプリング周波数の1/2の1000Hzでゲインゼロ
- 4回平均の場合は、サンプリング周波数の1/4の500Hzでゲインゼロ
- 8回平均の場合は、サンプリング周波数の1/8の250Hzでゲインゼロ
- 10回平均の場合は、サンプリング周波数の1/10の200Hzでゲインゼロ
となる。1/nも同様。
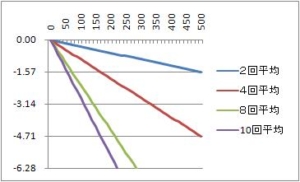
次に、縦軸の振幅をdB(デシベル)単位にする。つまり、上記グラフの縦軸の10底のlogをとって、20をかける。すると
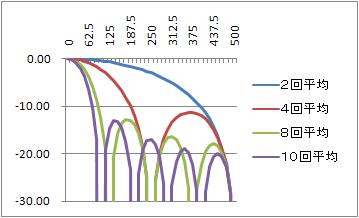
横軸は、周波数[Hz]。サンプリング周期は1ms。平均回数を増やしたほうが、シャープなローパスフィルタになる。
※エクセルの元データはこちらからダウンロードできます。
単純移動平均フィルタ位相特性 まとめ 比較 Excelデータ