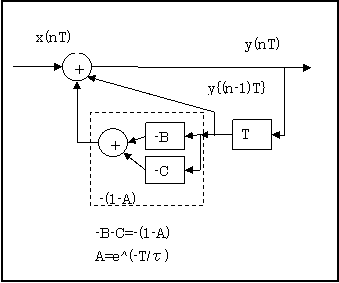前回までの振り返り
インパルス不変法で一次IIRローパスフィルタを設計して、
$$y(nT) = x(nT) + e^{-\frac{T}{\tau}} * y((n-1)T) (式8)$$
のフィルタ計算式を得た。
計算の導出については、以下の記事を参照
あわせて読みたい

【IIRフィルタ】第1回:インパルス不変法による一次IIRフィルタ設計(基本、初歩)
さて、FIRフィルタの次は、IIRフィルタを設計してみる。 FIRフィルタに関しては【FIRフィルタ】シリーズに詳しく書いてあります。 https://primemotion.com/filter FIR...
このブロック図は、以下のようになる。
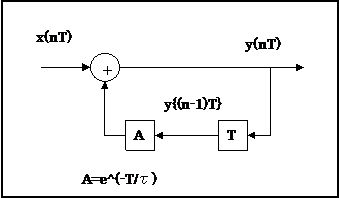
これを置き換えると、

となる。係数1-A えお右シフト演算を置き換えると
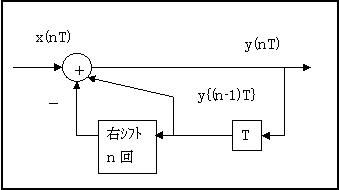
となる。
この右シフト回数nと、時定数τ、最終値の関係を表に示す。この表では、サンプリング周期T=1msとしている。
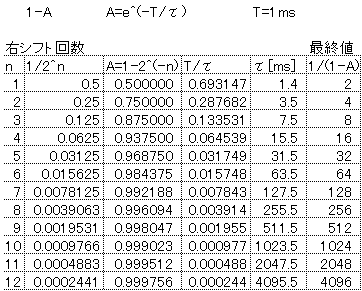
例えば、右シフト回数が4回、したがって、1/2^4=1/16=1-Aのとき、時定数τは約15.5msとなる。
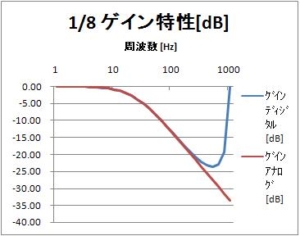
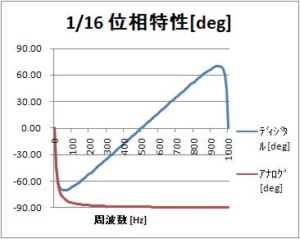
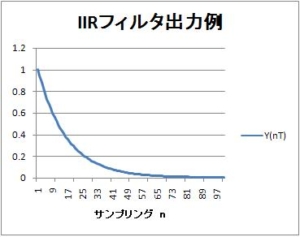
この係数のときのインパルス応答は、0に漸近しないで、15に落ち着いてしまうことに注意したい。これは1/16の整数演算で、15が桁落ちで後段に伝搬しないことによる。詳細は、以下の記事を参照されたい。
あわせて読みたい
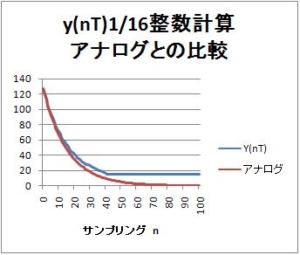

【IIRフィルタ】第3回:簡単一次IIRフィルタのインパルス応答波形
前回のおさらい 1次のIIRローパスフィルタは、以下の式で実現できる。 $$y(nT) = x(nT) - (1-e^{-\frac{T}{\tau}}) * y((n-1)T) + y((n-1)T) (式9)$$ ここで、例...
また、右シフト回数が4回、1/16演算をすると、フィルタ出力の最終値が分母の値16になることにも注意したい。
上記表のエクセルはこちら
一次IIRローパスフィルタの簡単実装まとめ Excelデータ1
次に、サンプリング周期Tを変えたら、どのような時定数$\tau$ が得られるか表に示す。
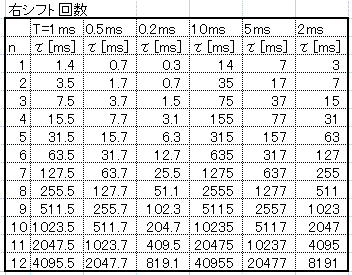
右シフト回数n=4にて、サンプリング周期T=2msならば、時定数$\tau$ =31msになる。
エクセルのデータはこちら
一次IIRローパスフィルタの簡単実装まとめ Excelデータ2
この表の時定数で満足できないときは、以下の計算ブロック図を試してみてほしい。つまり、B=1/8(右シフト3回)、C=1/16(右シフト4回)とすれば、中間の時定数が得られる。、