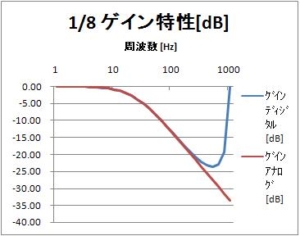
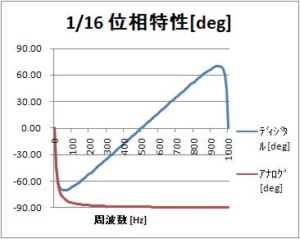
前回の記事に引き続き、簡単1次IIRローパスフィルタの波形を示す。
正弦波入力に対する応答波形を求める。
ディジタルフィルタ計算式は、
$$y(nT) = x(nT) – \frac{1}{8} * y((n-1)T) + y((n-1)T) (式24)$$
時定数は、約7msになる。
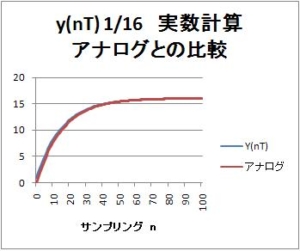
以下に示す波形の横軸はサンプリングn。サンプリング周期T=1msなら、横軸は時間[ms]。ディジタルフィルタの入力$x(nT)$は振幅127の正弦波である。ディジタルフィルタ出力$y(nT)$とグラフ中で比較するディジタルフィルタ入力は、振幅127正弦波に対して、8倍の振幅、すなわち$127 * 8 = 1016$の振幅にしている。8倍の「8」は、「最終値の定理」によって求められる値である。
最終値の定理については、以下の記事を参照してください。
100ms周期の正弦波に対する出力(整数計算)
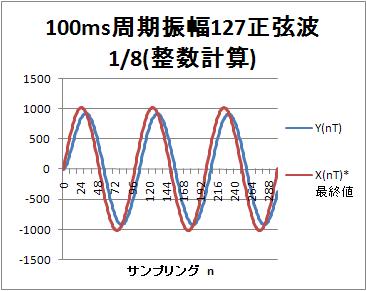
出力$y(nT)$の振幅は 918。入力との比は$918 /(127*8) = 0.90$になっている。
位相は7ms程度遅れているので、 7ms/100ms*360度 = 25度程度の遅れになっている。
20ms周期の正弦波に対する出力(整数計算)
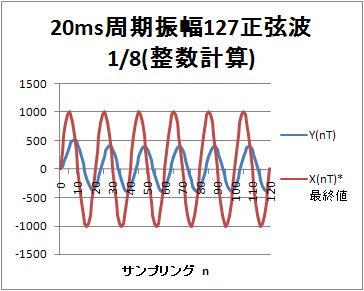
出力$y(nT)$の振幅は 396。入力との比は$396 /(127*8) = 0.39$になっている。
位相は約3.5ms程度遅れているので、 3.5ms/100ms*360度 = 63度程度の遅れになっている。
10ms周期の正弦波に対する出力(整数計算)
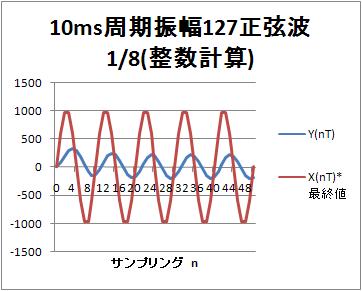
出力$y(nT)$の振幅は 212。入力との比は$212 /(127*8) = 0.21$になっている。
位相は1.5ms程度遅れているので、 1.5ms/10ms*360度 = 54度程度の遅れになっている。
5ms周期の正弦波に対する出力(整数計算)
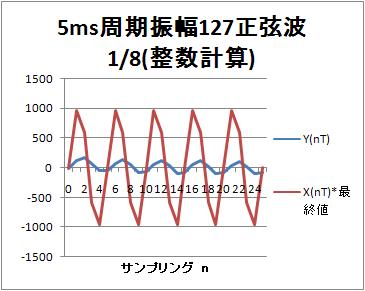
出力$y(nT)$の振幅は 105。入力との比は$105 /(127*8) = 0.10$になっている。
位相は1.5ms程度遅れているので、 1.5ms/5ms*360度 = 108度程度の遅れになっている。
エクセルのデータはこちら
係数1/8の一次IIRフィルタの正弦波入力応答 Excelデータ