先の記事に引きつづき、簡単1次IIRローパスフィルタの波形を示す。
今回のミッション
周波数特性を求める。
$$y(nT) = x(nT) – \frac{1}{8} * y((n-1)T) + y((n-1)T) (式24)$$
サンプリング周期T=1msとしたとき、時定数は、約7msになります。
周波数特性の計算式導出方法について、知りたい方は、以下の記事を参照願います。
あわせて読みたい


【IIRフィルタ】第7回:簡単一次IIRフィルタの周波数特性の計算式
さて、今回は、インパルス不変法で設計した一次のIIRローパスフィルタの周波数特性計算式を導きます。 ディジタルフィルタの計算式は、こちらの記事 https://primemotio...
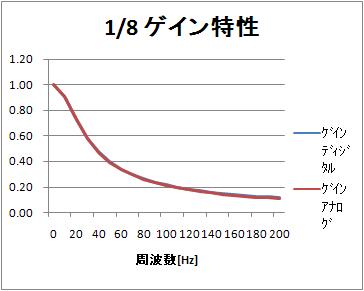
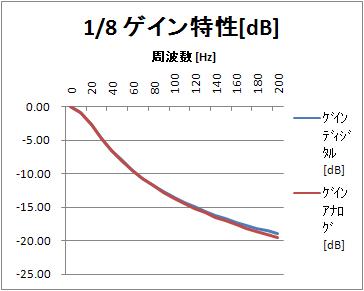
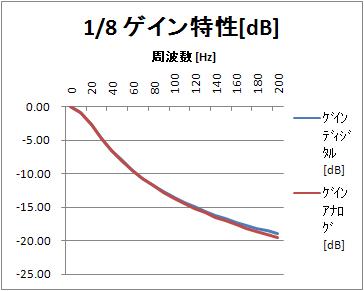
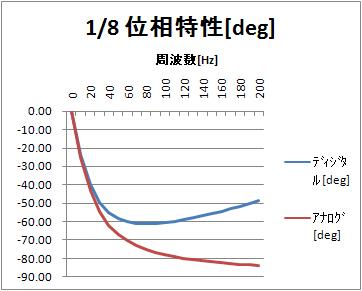
周波数特性のグラフは、以下になります。同じ時定数のアナログ一次ローパスフィルタのの周波数特性と比較しています。
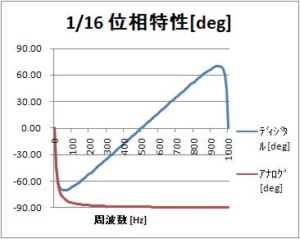
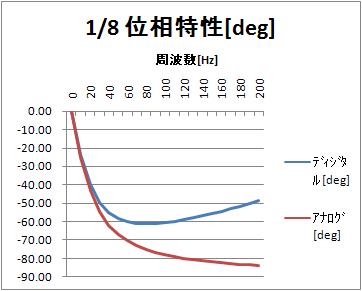
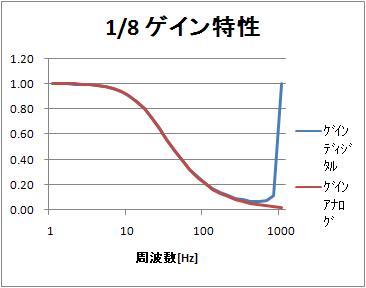
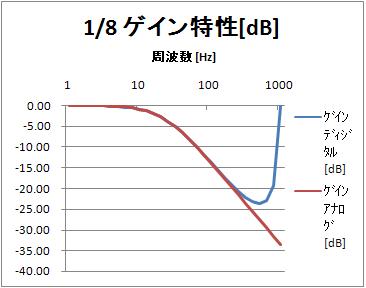
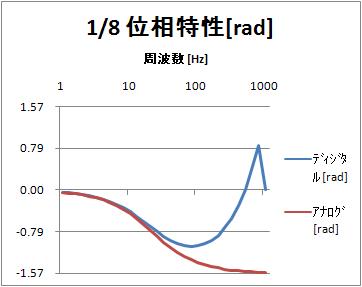
振幅特性は似ているけれど、位相特性は違いますね。
振幅特性(リニア周波数軸)
振幅特性[dB](リニア周波数軸)
位相特性[rad](リニア周波数軸)
位相特性[deg](リニア周波数軸)
エクセルのファイルはこちら
係数1/8の一次IIRフィルタの周波数特性 Excelデータ1
つぎに周波数軸をlog軸にした波形も合わせて示します。
振幅特性(log周波数軸)
振幅特性[dB](log周波数軸)
位相特性[rad](log周波数軸)
位相特性[deg](log周波数軸)
エクセルのデータはこちら
係数1/8の一次IIRフィルタの周波数特性 Excelデータ2