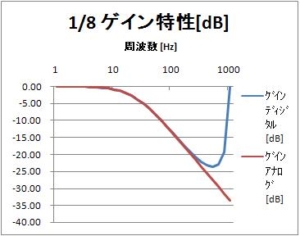
前回のおさらい
一次遅れのIIRフィルタの計算式は
$$y(nT) = x(nT) + e^{-\frac{T}{\tau}} * y((n-1)T) (式8)$$
となる。
さて、係数の$e^{-\frac{T}{\tau}}$は、どんな値になるだろうか?たとえば、サンプリング周期T=1ms、設計したいフィルタの時定数$\tau = 10$ msとすると、$e^{-0.1}=0.90483$ となる。
$0.904837$ をどのように扱うか?
試しに、この値を1から引いてみよう。
$$1 – 0.904837 = 0.095163$$
約1/10.5。1/16としてしまえば、右シフト演算4回で行ける。割り算よりシフト演算なら格段に速い。VHDLやVerilogでも簡単に記述実装できる。
そうか!
係数を$e^{-\frac{T}{\tau}}$ではなくて、$1-e^{-\frac{T}{\tau}}$ の形になるようにすれば簡単な演算になるのだ。(式8)を係数$1-e^{-\frac{T}{\tau}}$になるよう変形してみる。
$$y(nT) = x(nT) – (1-e^{-\frac{T}{\tau}}) * y((n-1)T) + y((n-1)T) (式9)$$
これをブロック図に書くと、
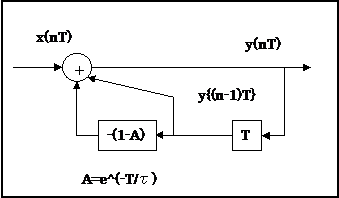
実装例、入出力時間波形、周波数特性については、次回以降で説明します。お楽しみに!