1次のIIRローパスフィルタは、以下の式で実現できる。
$$y(nT) = x(nT) – (1-e^{-\frac{T}{\tau}}) * y((n-1)T) + y((n-1)T) (式9)$$
ここで、例として係数を
$$1-e^{-\frac{T}{\tau}} = \frac{1}{16} (式10)$$
としてみよう。4回右シフトで1/16を実現しようともくろんでいる。
$$1 – \frac{1}{16} = e^{-\frac{T}{\tau}}$$
両辺の自然対数をとって、
$$-\frac{T}{\tau} = \ln{(1 – \frac{1}{16})} $$
$$\tau = -\frac{T}{\ln{(1 – \frac{1}{16})}}$$
$$ = T * 15.4946$$
となる。サンプリング周期T=1msとすれば、時定数$\tau =15.49$ msのディジタルフィルタが実現できる。 (式9)は、(式10)と置いたので
$$y(nT) = x(nT) – (1- \frac{1}{16} * y((n-1)T) + y((n-1)T) (式11)$$
となる。これを、実際に計算してみよう。
まず、入力$x(nT)$として、パルスを入力してみよう。
最初の1サンプリングだけ、1。あとは、ずっと0。式にすると、
$$x(nT) = 1 (n=0)$$
$$x(nT) = 0 (n=1,2,3,,,)$$
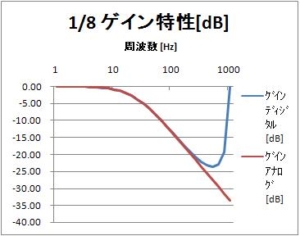
この場合の出力$y(nT)$は、以下のグラフになる。1/16の計算で小数点以下が発生するが、実数で計算している。アナログフィルタ出力の理想波形
$$y(t) = e^{-\frac{t}{0.0154946}}$$
と比較している。

横軸はサンプリングn。サンプリング周期T=1msの場合は、時間[ms]と考えて良い。アナログ波形とディジタル演算波形に、ほとんど差がない。どのくらい差があるか知りたい方は、追って、エクセルデータをアップロードするのでみてください。
次に整数計算してみる。途中の1/16で桁落ち(小数点以下は無視される)ので、入力x(nT)を大きい値にする。ここでは、127にする。つまり、最初の1サンプリングだけ、127。あとは、ずっと0。式にすると、
$$x(nT) = 127 (n=0)$$
$$x(nT) = 0 (n=1,2,3,,,)$$
この場合の出力$y(nT)$は、以下のグラフになる。アナログの理想波形と比較している。横軸はサンプリングn。サンプリング周期T=1msの場合は、時間[ms]と考えて良い。
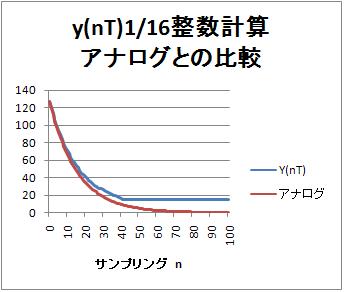
出力$y(nT)$が0にならないことがわかる。15で落ち着いてしまう。理由は、途中の1/16演算に15が入力されても、演算結果が0になってしまい、出力に現れないことによる。
つまり、1/16を途中に入れると、16より1少ない15が誤差として残る。
使えるか?
16bit($-32768$から$+32767$)等の有限桁数のデバイスで実装を狙っているので、誤差はやむを得ないという前提である。誤差15が気にならないように16倍したデータを$x(nT)$に入力すれば、誤差の割合は減る。つまり、精度は上がる。
あとで説明するかもしれないが、1/32を途中に入れると、32より1少ない31が誤差として残る。同様に1/8を途中に入れると、8より1少ない7が誤差として残る。
なお、今は、サンプリング周期T=1msとして、時定数$\tau = 15.49$msとなっているが、
- サンプリング周期を1/10にして、T=0.1msなら、時定数は、1/10の$1.549$ms
- サンプリング周期を10倍にして、T=10msなら、時定数は、10倍の$154.9$ms、
どんなサンプリング周期でも$15.49$倍である。
次の記事では、ステップ応答の波形を計算する。