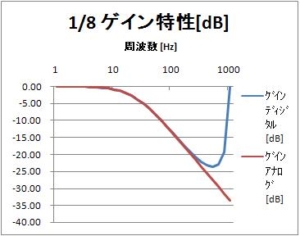
1次IIRフィルタで、サンプリング周期T=1ms、時定数 $\tau$=15ms程度のローパスフィルタを実装しようとしている。
計算式はさきの記事より、
$$y(nT) = x(nT) – (1- \frac{1}{16} * y((n-1)T) + y((n-1)T) (式11)$$
インパルス応答を先の記事で計算したので、今日は、ステップ応答を計算してみよう。
まず、入力$x(nT)$は、ずっと1。式にすると、
$$x(nT) = 1 (n=0,1,2,,,)$$
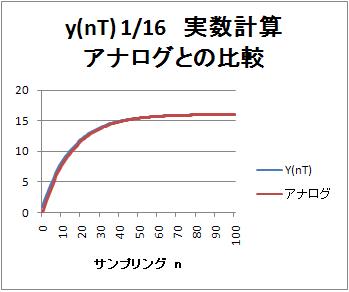
これを入力として、(式11)のディジタルフィルタ出力$y(nT)$を計算すると16に近づく。
$$y(nT) → 16$$
この値は、最終値の定理として知られている計算式からも得られる。
フィルタの伝達関数を$G(z)$として、値が1のステップ入力を入力したとき、出力$y(nT)$の最終値は、
$$\lim_{x \to \infty}y(nT) = \lim_{z \to 1}(z-1) * G(z) * \frac{z}{z-1}$$
$$= \lim_{z \to 1}z * G(z)$$
今計算しているディジタルフィルタの伝達関数は、先の記事
の(式5)より、
$$G(z) = \frac{1}{1 – e^{-\frac{T}{\tau}} * z^{-1}} (式5)$$
である。これを代入して、$y(nT)$の最終値は
$$\lim_{n \to \infty}y(nT) = \lim_{z \to 1}\frac{z}{1 – e^{-\frac{T}{\tau}} * z^{-1}}$$
$$= \frac{1}{1 – e^{-\frac{T}{\tau}}}$$
先の記事で、簡単な演算を目論んで
$$1 – e^{-\frac{T}{\tau}} =\frac{1}{16}$$
と置いたので、$y(nT)$ の最終値は、16となる。
グラフの比較波形として、アナログ波形を載せるが、最終値を一致させて比較しやすくするために、値16のステップ入力を入れたアナログ1次ローパスフィルタ出力波形
$$y(t) = 16 * (1-e^{-\frac{t}{15.4946E-3}})$$
を示している。$15.4946E-3$は、ディジタルフィルタ設計式から得られた時定数である。約15ms。
計算の途中、1/16で桁落ちするので、x(nT)として、127を入力している。式としては、
$$x(nT) = 127 (n=0,1,2,,,)$$
最終値は、127の入力に変わったので、$127*16=2032$である。
比較用のアナログ波形は、最終値を合わせるために
$$y(t) = 127 * 16 * (1-e^{-\frac{t}{15.4946E-3}})$$
を示している。
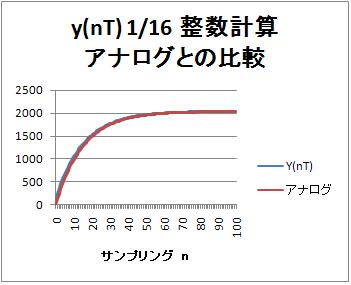
おおむね同じ波形になる。横軸はサンプリング、T=1msの場合は、時間[ms]。
差異に興味ある方は、エクセルのデータをみてね。データはこちら、
簡単一次IIRフィルタのステップ応答波形 Excelデータ
最終値の定理は、例えば、横山、佐川、貴家の訳;「ディジタル制御システム 解析と設計」、日刊工業新聞社、1990年、33ページに載っている。