最近の記事では、一次のIIRフィルタで簡単なローパスフィルタを設計している。計算式は、しばらく前の記事から、
最近の記事では、一次のIIRフィルタで簡単なローパスフィルタを設計している。
計算式は、しばらく前の記事から、
$$y(nT) = x(nT) – (1-e^{-\frac{T}{\tau}}) * y((n-1)T) + y((n-1)T) (式9)$$
である。計算の簡単化のために、係数1/16を使用して、時定数τは約15msである。
インパルス応答、ステップ応答は、先の記事で計算してみた。
今回は、正弦波入力$x(nT)$を入れた応答出力$y(nT)$を計算する。
いずれも、サンプリング周期T=1ms、横軸は時間[ms]である。
実数演算と整数演算を比較して示す。整数演算の場合の正弦波振幅は127として、整数に丸めた入力を使用している。同様に整数演算1/16の出力も整数に丸めている。また、いずれの波形においても、入力を16倍にした出力(理想波形出力)と比較している。16倍の16は、先の記事で書いたように最終値の定理で求められる。
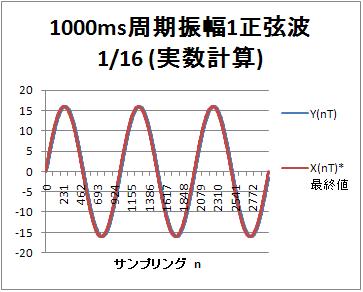
実数演算
整数演算
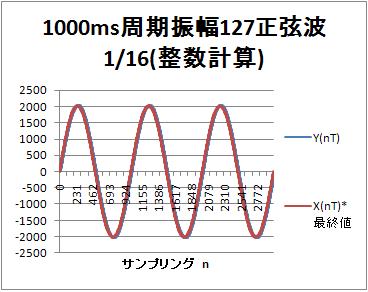
時定数15msのローパスフィルタに対して、1000ms周期を正弦波を入力した場合、出力の振幅、位相ともに入力に対して大きな変化がない。
実数計算、整数計算の大きな差もない。
差異の詳細については、追ってアップロードするエクセルファイルを見てください。
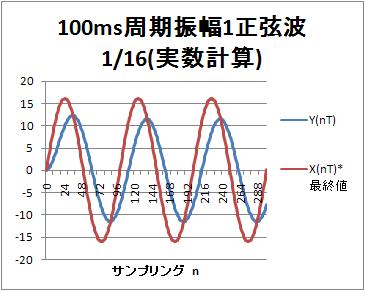
実数演算
整数演算
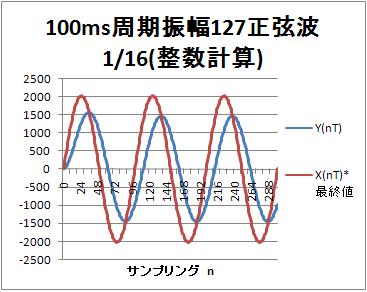
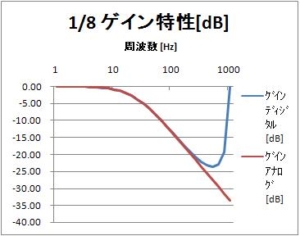
出力振幅は2032の期待に対して、実際は1454であり、約0.721になっている。位相は12msほど遅れている。周期100msに対して、位相遅れを計算すると、12ms/100ms*360°=43°程度になる。
後日、アップロード予定のゲイン特性の10Hz(周期100ms)計算値は、0.717であり、上記の約0.721と一致している。また、位相特性の100Hz計算値は、-42°で、上記の43°程度と一致している。
別の周波数の正弦波入力に対する出力波形は、次の記事で。