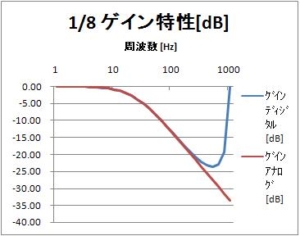
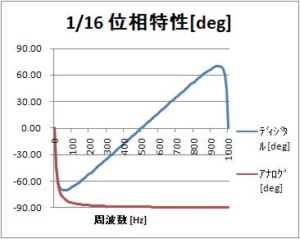
前回の記事で、インパルス不変法で設計した一次IIRローパスフィルタの振幅特性や位相特性のグラフを紹介した。

ディジタルフィルタの計算式は、
$$y(nT) = x(nT) – \frac{1}{16} * y((n-1)T) + y((n-1)T) (式11)$$
で、係数を1/16として、シフト演算を使えるようにしている。
サンプリング周期T=1msの場合、一次IIRフィルタの時定数は、$15.4946$[ms]となる。詳細は
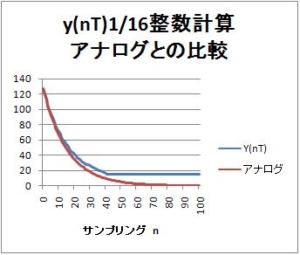
を参照。
今日は、そのグラフを同じ時定数のアナログローパスフィルタと比較してみる。さて、一次ローパスフィルタの伝達関数は、時定数を$\tau$[s]として
$$G(s) = \frac{1}{1 + s\tau} (式20)$$
$s = j\omega$ を代入して、$\omega$ の関数にする。
$$G(j\omega) = \frac{1}{1 + j\omega \tau}$$
$$ = \frac{1}{\sqrt{1 + (\omega \tau)^{2}}} * e^{j\phi(\omega)} (式21)$$
ここで、位相は
$$\phi(\omega) = arctan(\omega\tau) (式22)$$
絶対値の部分をとって、ゲインは
$$g(\omega) = \frac{1}{\sqrt{1 + (\omega\tau)^{2}}} (式23)$$
時定数$\tau$ は前述のように
$$\tau = 15.4946E-3$$
同じ時定数のアナログローパスフィルタの位相特性(式22)、ゲイン特性(式23)が得られたので、前回の記事で導出した一次IIRローパスフィルタの振幅特性や位相特性を比較してみる。
グラフは、
- 細かい部分がわかるように、0~200Hz のグラフ
- サンプリング周波数1000Hz までがわかるように、0~1000Hzのグラフ
を示す。
ゲイン特性(0~200Hz)
比較のため、ディジタルのゲイン特性を正規化して(直流でのゲインの値、16ですべてのゲイン値を割って)いる。
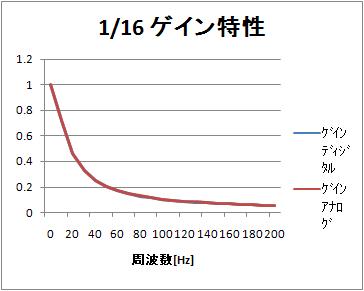
200Hz まではほとんど差がない。
ゲイン特性(0~1000Hz)
サンプリング周期T=1msとしているので、1000Hzはサンプリング周波数である。
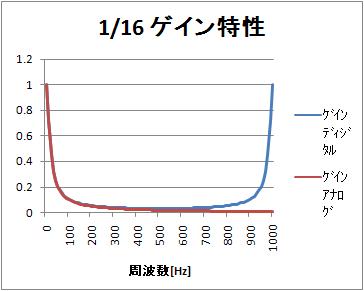
サンプリング周波数1000Hzの半分、500Hzからずれてくる。
ゲイン特性[dB](0~200Hz)
次に縦軸をデシベル[dB]にしてみる。
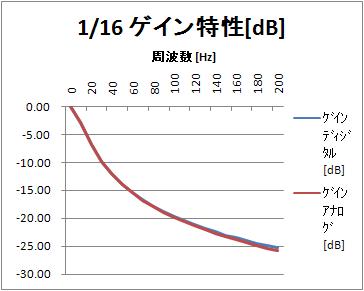
ゲイン特性[dB](0~1000Hz)
サンプリング周期T=1msとしているので、1000Hzはサンプリング周波数である。
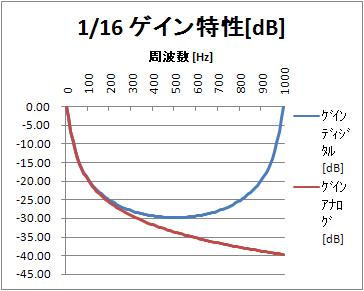
位相特性[rad](0~200Hz)
次は、位相特性を見てみる。

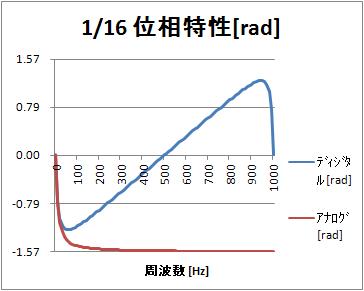
位相特性[rad](0から1000Hz)
サンプリング周期T=1msとしているので、1000Hzはサンプリング周波数である。
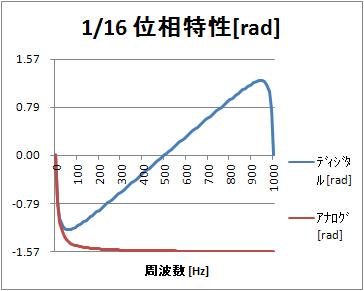
位相特性[rad](0~1000Hz)
サンプリング周期T=1msとしているので、1000Hzはサンプリング周波数である。
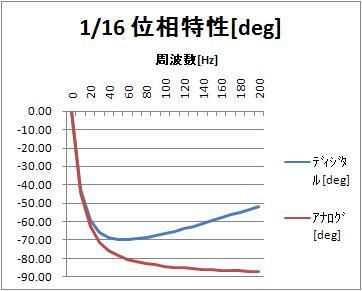
位相特性[deg](0~200Hz)
次に縦軸を度[deg]にしてみる。
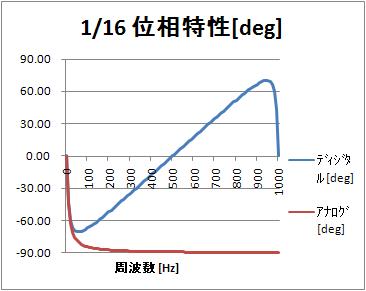
位相特性[deg](0~1000Hz)
サンプリング周期T=1msとしているので、1000Hzはサンプリング周波数である。
エクセルのデータはこちら
簡単一次IIRフィルタの周波数特性のグラフ(アナログフィルタとの比較) Excelデータ