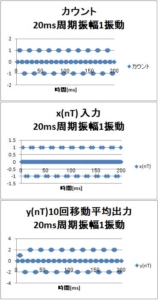
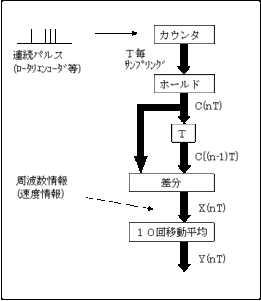
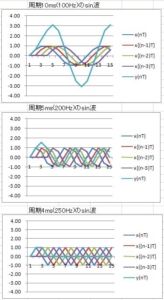
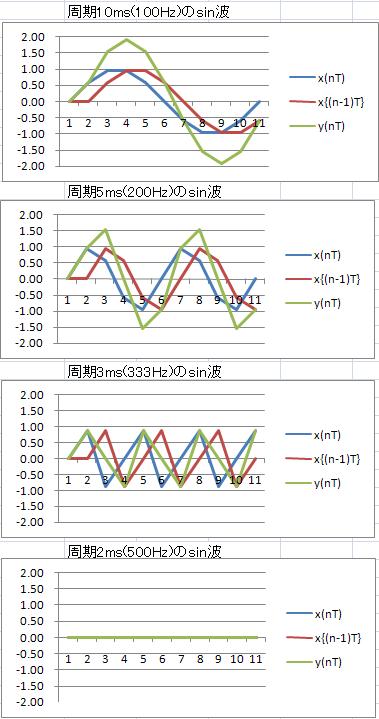
次に、1000Hz サンプリング(制御周期1ms)の2回移動平均フィルタに 100Hz、200Hz、333Hz、500Hz $sin$波入力した場合の、$入力x(nT)、出力y(nT)、内部状態のx((n-1)T)$ を示す。横軸の単位はms。
以下は、$x(nT)$ を正弦波として、
$$y(nT) = x(nT) + x((n-1)T) $$
を計算したグラフである。
結果は…
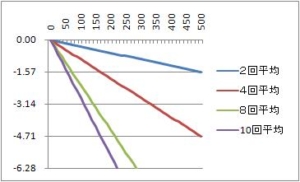
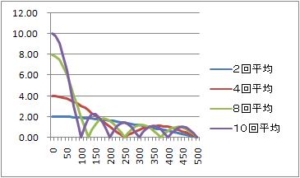
- サンプリング周波数1000Hz の1/10 の100Hz の正弦波を2回移動平均フィルタへ入力すると、出力振幅が入力の約2倍になる。
- サンプリング周波数1000Hz の1/5 の200Hz では、出力振幅が入力の約1.5倍。
- サンプリング周波数1000Hz の1/3 の333Hz では、出力振幅が入力の約1倍。
- サンプリング周波数1000Hz の1/2 の500Hz では、出力はゼロ。フィルタリングされる。
たとえば、サンプリング周波数が2倍の2000Hz(制御周期500us)のとき、やはり、サンプリング周波数2000Hzの”1/2”の1000Hzでは、出力がゼロになる。
読者のみなさんのシステムのサンプリング周波数が1000Hzのn倍だったら、特性はn倍の周波数に拡大されると考えてください。1/nでも同様。
※エクセルの元データはこちらダウンロードできます。