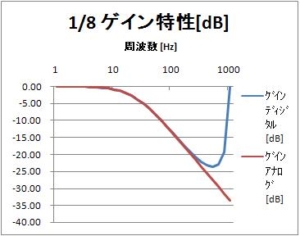
今日は、一次のIIRフィルタの周波数特性のグラフを示す。
ゲイン特性の計算式は、前回の記事より
$$g(\omega) = \frac{1}{\sqrt{(1 – Acos\omega T)^{2} + (Asin\omega T)^{2})}} (式18)$$
位相特性の計算式は、前回の記事より
$$\phi(\omega) = -\arctan(\frac{Asin\omega T}{1 – Acos\omega T}) (式19)$$
ここで、
$$A = e^{-\frac{T}{\tau}} (式13)$$
Tはサンプリング周期、$\tau$ は時定数。
以下のグラフでは、
$$1 – A = 1 – e^{-\frac{T}{}\tau} = \frac{1}{16}$$
としてあります。
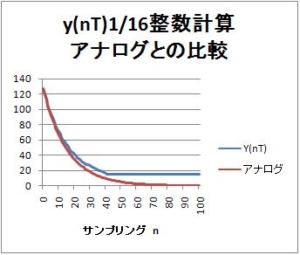
の記事の
$$1 – e^{-\frac{T}{\tau}} = \frac{1}{16} (式10)$$
ここで、サンプリング周期T = 1ms とすれば、時定数$\tau$ は約15msとなります。
ゲイン特性
周波数が上がるとゲインが小さくなります。周波数が高い正弦波をこのフィルタに入れると、出力波形の振幅が小さくなります。ローパスフィルタを設計したのだから、当然ですね。
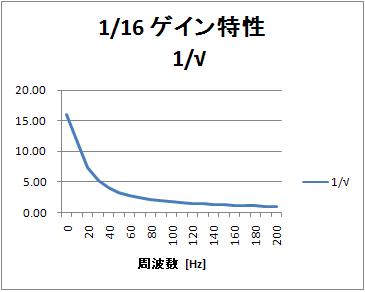
実際の入力の正弦波と出力の正弦波については、先の記事

を参照して下さい。
ゲイン特性 [dB]
デシベル[dB]に直しました。
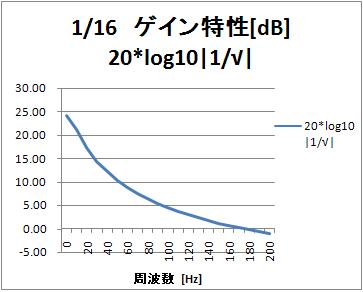
位相特性 [rad]
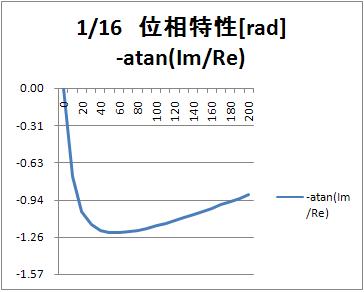
周波数が上がると位相が次第に遅れます。しかし、さらに周波数が上がると位相遅れが小さくなります。おもしろいですね。
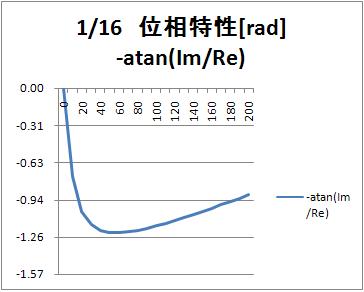
位相特性 [deg]
度で計算しました。
エクセルのデータは、こちら
簡単一次IIRフィルタの周波数特性のグラフ(アナログフィルタとの比較) Excelデータ
今回、サンプリング周期T=1msとして、時定数$\tau$が約15msになっていますが、
サンプリング周期を長くして、T=10msとすれば、時定数$\tau$が約150msとなります。周波数特性のグラフは同じ形になりますが、横軸の周波数最大値は200Hzを20Hzとして考えてください。
逆にサンプリング周期を短くして、T=0.1msとすれば、時定数$\tau$が約1.5msとなります。周波数特性のグラフは同じ形になりますが、横軸の周波数最大値は200Hzを2000Hzとして考えてください。
今回のディジタルフィルタの計算式は
$$y(nT) = x(nT) -farc{1}{16} * y((n-1)T) + y((n-1)T) (式11)$$
です。
乗算器や浮動小数点演算を使用しないで、シフト演算だけで一次IIRフィルタを実現しました。これなら、安いマイコンやVHDL、verilogで実現できますよね。
これから、今回のサンプリング周期T=1ms、時定数$\tau$ 約15ms以外についても考えていきます。