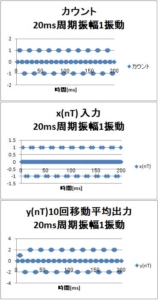
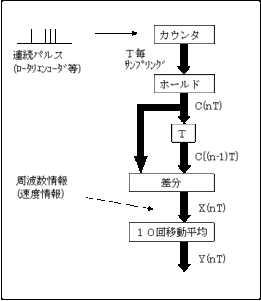
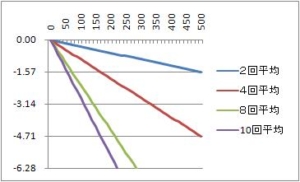
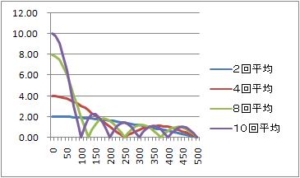
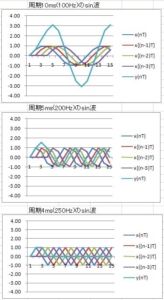
仕事で、移動平均の周波数特性の検討書を作ることになったので、昔勉強した本を引っ張りだして、書いている。「移動平均」は、株価の分析にも出てくる。ここでは、ディジタル信号処理のローパスフィルタとして使用する。まず、簡単な2回移動平均から。FIRフィルタのもっとも簡単な形。
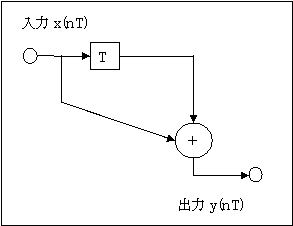
■図の入出力関係は
$$y(nT) = x(nT) + x{(n-1)T} (式1)$$
■伝達関数を求める。(式1)の両辺をまずZ変換する。
$$y(nT) => Y(z), x(nT) => X(z), x{(n-1)T} => X(z) * z^{-1}$$
と置き換える。すると
$$Y(z) = X(z) + X(z) * z^{-1}$$
次に、出力 Y(z) と X(z) の比の形に変形する。
$$Y(z) / X(z) = 1 + z^{-1} (式2)$$
これが伝達関数である。
■次に周波数特性を求める。伝達関数の式において、$z^{-1}$ を $e^{-jwT}$ に置き換える。左辺の $z$ は、$e^{jwt}$ に置き換える。$w$ は角周波数。$T$ はサンプリング周期。株式市場なら、1日。速度制御なら 1ms から 数百 μs あたり。
$$Y(e^{jωT}) / X(e^{jωT}) = 1 + e^{-jωT}$$
これを振幅と位相の式に変形する。複素数に関わる知識が必要になる。オイラーの公式
$$e^{jθ} + e^{-jθ} = 2*cosθ$$
を使えるように変形する。
$$(e^{jωT/2} + e^{-jωT/2}) * e^{-jωT/2 }$$
上記のオイラーの式を使って、
$$Y(e^{jωT}) / X(e^{jωT}) = 2 * cos(ωT/2 ) * e^{-jωT/2} (式3)$$
これが、2回移動平均の周波数特性である。