【FIRフィルタ】第13回：移動平均フィルタによる速度検出フィルタ(周波数検出フィルタ)

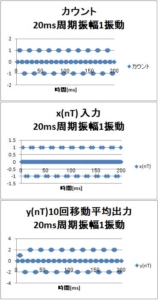
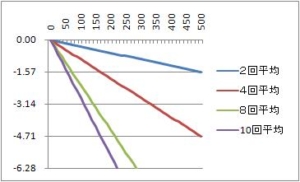
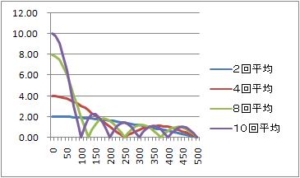
今回は、移動平均フィルタへの入力を変えてみる。いままでの記事では、正弦波入力波形を示してきた。今回は、周波数検出、速度検出を意識して、パルスを入力してみる。

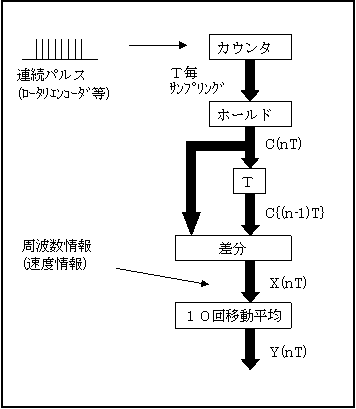
一定周波数のパルスをカウントして、一定周期Ｔ毎、その差分を取る(引き算をする)。

$$x(n) = c(nT) – c((n-1)T)$$

これは、周波数検出になる。もし、そのパルス発生源がロータリエンコーダやリニアスケールならば、速度検出になる。このカウンタの差分データを１０回移動平均に入力してみる。

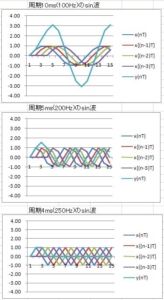
サンプリング周期T=1ms、すなわち、サンプリング周波数1000Hzとして、いろいろな周波数を入力し、１０回移動平均入力の$x(nT)$と、移動平均出力の$y(nT)$を以下に比較する。横軸は時間[ms]、縦軸は$x(nT)$もしくは$y(nT)$。

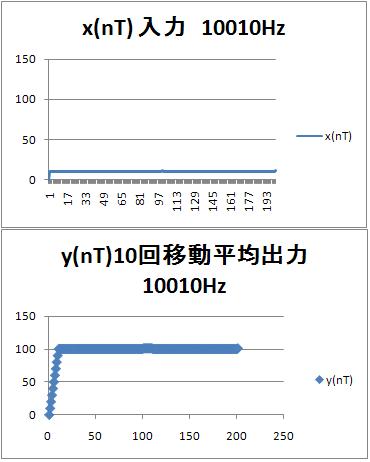
10010Hzのパルス入力に対する$x(nT)$と$y(nT)$

入力$x(nT)$、出力$y(nT)$ともの１のずれがある。入力$x(nT)$では平均10に対して１、出力$y(nT)$では平均100に対して１、なので、フィルタを通したことによりS/N比（信号とノイズの比）が１０倍改善されている。

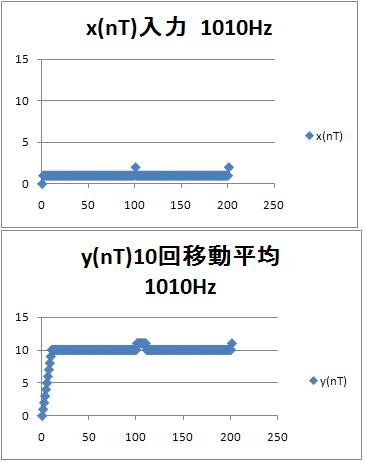
1010Hzのパルス入力に対する$x(nT)$と$y(nT)$

入力$x(nT)$、出力$y(nT)$ともの１パルスのずれがある。入力$x(nT)$では平均1に対して１、出力$y(nT)$では平均10に対して１、なので、フィルタを通したことによりS/N比（信号とノイズの比）が１０倍改善されている。

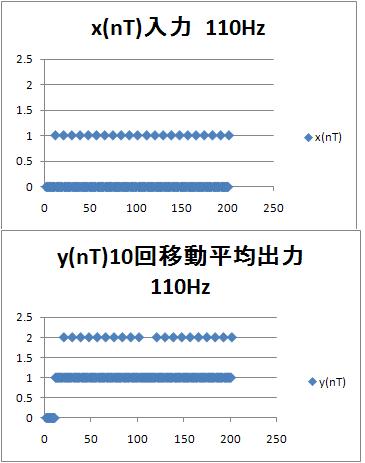
110Hzのパルス入力に対する$x(nT)$と$y(nT)$

入力$x(nT)$、出力$y(nT)$ともの１パルスのずれがある。入力$x(nT)$では0に対してたまに１、出力$y(nT)$では1に対してたまに１、なので、フィルタを通したことによりS/N比（信号とノイズの比）が改善されている。

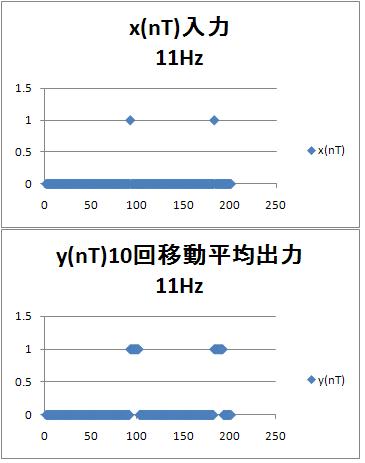
11Hzのパルス入力に対する$x(nT)$と$y(nT)$

入力$x(nT)$、出力$y(nT)$ともの１パルスのずれがある。入力$x(nT)$では0に対してたまに１、出力$y(nT)$では0に対してたまに１、なので、フィルタを通したことによりS/N比（信号とノイズの比）改善効果は、ない。

エクセルの元データはこちら
移動平均フィルタによる速度検出フィルタ（周波数検出フィルタ）Excelデータ

本記事では、定速時の動作について計算した。＋１、－１、＋１と振動している場合の動作については、次の記事で。