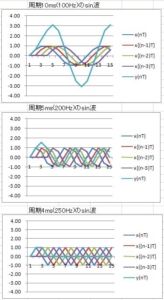
前回のおさらい
2回移動平均の周波数特性は、
$$Y(e^{jωT}) / X(e^{jωT}) = 2 * cos(ωT/2) * e^{-jωT/2} (式3)$$
である。
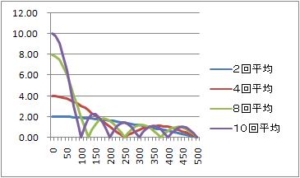
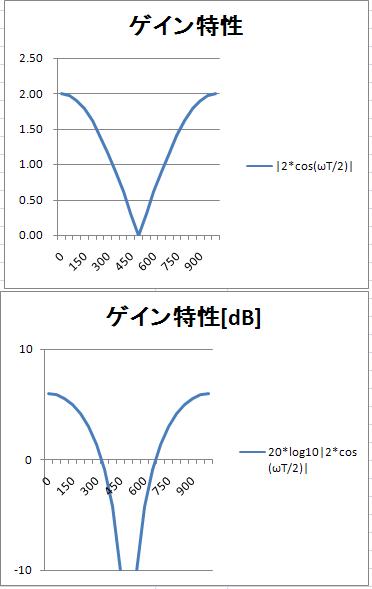
この式の振幅部分($e^x$ 以外の部分)を切り出して、絶対値にするとゲイン特性(振幅特性)は
$$g(ω) = | 2 * cos(ωT/2) | (式4)$$
具体的な例として、サンプリング周期1000Hz(制御周期1ms)、横軸周波数のグラフにする。グラフからサンプリング周期の半分 500Hz でゲインがゼロ、つまり、500Hz の制限は信号は出力に現れない。フィルタリングされる。サンプリング周期の 1/10 の 100Hz の正弦波信号は入力の 1.9倍になって、出力に現れる。また、0Hz、すなわち直流は、2倍になって現れる。
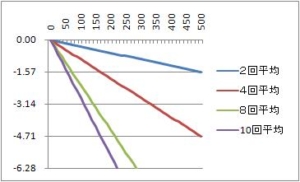
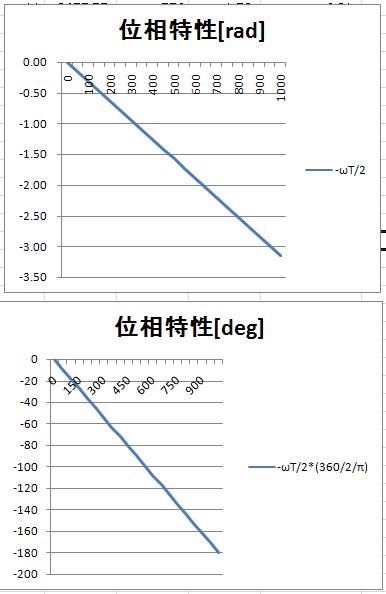
同じく、位相部分($e$ の指数部分の $j$ を除いた値)を取り出して、
$$φ(ω) = -ωT/2 [rad] (式5)$$
同じく、サンプリング周期1000Hz(制御周期1ms)、横軸周波数のグラフにする。サンプリング周期の1/10 の100Hz の信号は、位相が18°遅れて出力に現れる。
※エクセルの元データはこちらからダウンロードできます。