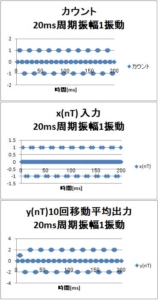
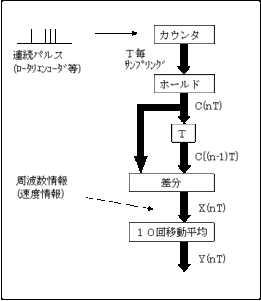
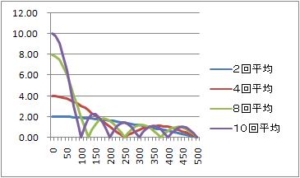
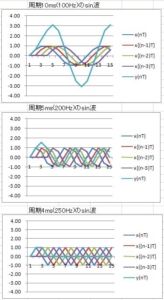
次は、4回の単純移動平均をしてみよう。
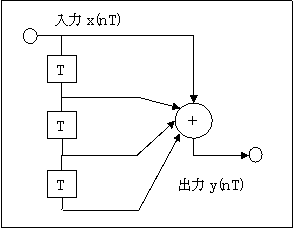
■図の入出力関係は
$$y(nT) = x(nT) + x((n-1)T) + x((n-2)T) + x((n-3)T) (式1)$$
■伝達関数を求める。(式1)の両辺をまずZ変換する。
$$y(nT) => Y(z) , x(nT) => X(z) , x((n-1)T)) => X(z)*z^{-1} , $$
$$x((n-2)T)) => X(z)*z^{-2} , x((n-3)T)) => X(z)*z^{-3}$$
と置き換える。すると
$$Y(z) = X(z) + X(z)*z^{-1} + X(z)*z^{-2} + X(z)*z^{-3}$$
$$= X(z) * { 1 + z^{-1} + z ^{-2} + z^{-3} }$$
次に出力$Y(z)$と$X(z)$の比の形に変形する。
$$Y(z)/X(z) = 1 + z^{-1} + z ^{-2} + z^{-3} (式2)$$
これが伝達関数である。簡単のため、$Y(z) / X(z) = G(z)$とおくと、
$$G(z) = 1 + z^{-1} + z ^{-2} + z^{-3} (式3)$$
これは、等比級数である。これをまとまった形に変形する。(式3)の両辺に$z^{-1}$をかけると、
$$G(z)*z^{-1} = z^{-1} + z ^{-2} + z^{-3} + z^{-4} (式4)$$
(式3)の両辺から、(式4)の両辺を引いて
$$G(z) – G(z)*z^{-1} = 1 – z^{-4}$$
$G(z)$について整理すると、
$$G(z) = (1 – z^{-4})/(1 – z^{-1}) (式5)$$
■次に周波数特性を求める。伝達関数の式において、$z^{-1}$を$e^{-jωT}$に置き換える。左辺の$Z$は、$e^{jωT}$に置き換える。$ω$は角周波数。$T$はサンプリング周期。
$$G(e^{jωT}) = (1 – e^{-jω4T})/(1 – e^{-jωT}) (式6)$$
(式6)の分子は、オイラーの公式
$$sinθ = ( e^{jθ} – e^{-jθ}) / 2j$$
を使って、
$$1 – e^{-jω4T} = e^{-jω2T} * (e^{jωT} – e^{-jωT})$$
$$= 2j * e^{-jω2T} * ( e^{jωT} – e^{-jωT} ) / 2j$$
$$= 2j * e^{-jω2T} * sin(2ωT)$$
となる。
(式6)の分母も同様に、分子に対して$4T$が$T$になっただけなので
$$1 – e^{-jωT} = 2j * e^{-jωT/2} * sin(ωT/2)$$
となる。したがって、(式6)は、
$$G(e^{jωT}) = sin(2ωT)÷[sin(ωT/2)* e^{-jωT3/2}] (式7)$$
これが周波数特性である。
■参考
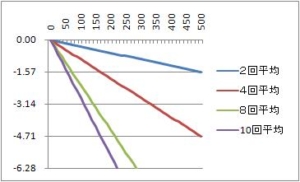
2回移動平均の周波数特性はこちらの記事を確認