単純4回移動平均の周波数特性は、下式であることがわかった。
$$G(e^{j\omega T}) = \frac{sin(2\omega T)}{sin(\omega T/2)} * e^{\frac{-3j\omega T}{2}} (式7)$$
この式の振幅部分(e^以外の部分)を切り出して、絶対値にするとゲイン特性(振幅特性)は、
$$g(\omega) = \frac{|sin (2\omega T)|} {|sin (\omega T/2)|} (式8)$$
ω=0のときは右辺は0/0になるので、その時の値は分子と分母を各ωで微分して、ω=0を代入して
$$lim_{\omega \to 0}\frac{2T * cos(2\omega T)}{\frac{T}{2}*cos(\frac{\omega T}{2})} = 4 (式9)$$
になる。
詳細は、森口、宇田川、一松:「数学公式Ⅰ~微分積分・平面曲線~」、岩波全書、42ページ(1981年17刷)を参照して下さい。今は、新しい版になっています。
あるいは、公式
$$sin4θ = 8sinθ(cosθ)^{3} – 4sinθcosθ (式10)$$
を(式8)の分子に用いて、ゲイン特性を
$$g(\omega) = 8 * (cos(\omega T/2))^{3} – 4 * cos(\omega T/2) \text{(式11)}$$
としてもよい。
上述の$sin4θ$の公式は、森口、宇田川、一松:「数学公式Ⅱ-級数・フーリエ解析-」、岩波全書、186ページ(1979年17刷)を参照してください。いまは、新しい版になっています。
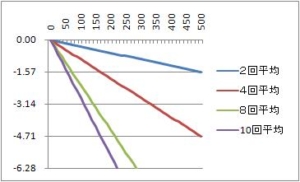
位相特性は、(式7)の位相部を切り出して
$$φ(\omega) = \frac{-3\omega T}{2} (式12)$$
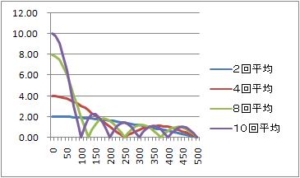
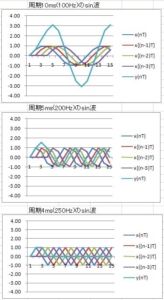
具体的な例として、サンプリング周期を1000Hz(制御周期1ms)、横軸周波数グラフにする。グラフからサンプリング周期の1/4の250Hzでゲインがゼロ。フィルタリングされる。サンプリング周期の1/10の100Hzの正弦波信号は入力の約3倍になって、出力現れる。0Hz、すなわち、直流は、4倍になって現れる。
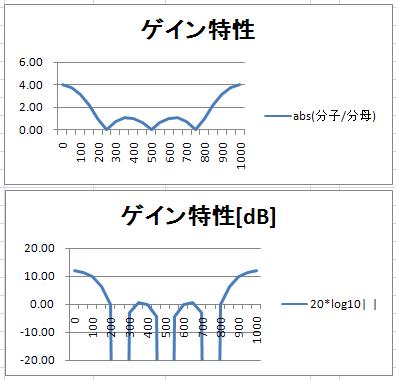
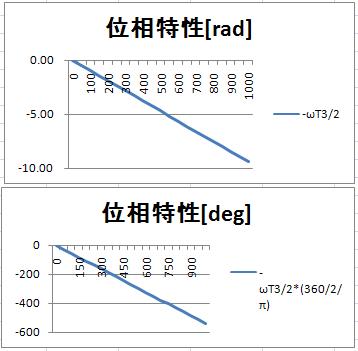
※エクセルの元データはこちらからダウンロードできます。
単純移動平均フィルタのゲイン特性と位相特性(4回平均)Excelデータ