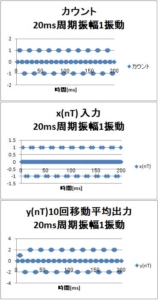
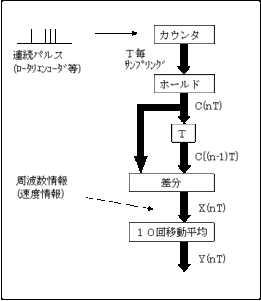
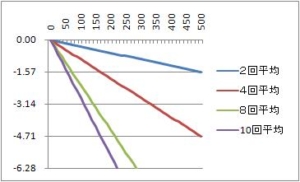
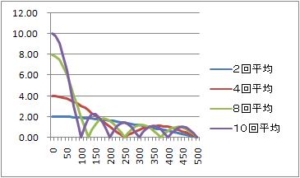
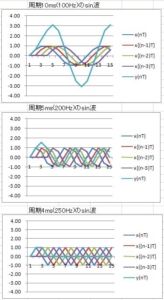
単純移動平均周波数特性のまとめ
先の記事の伝達関数 $G(z)$ の $z$ に $z=e^{jωT}$ を代入して、オイラーの公式を利用して、式を整理する。
2回平均
$$G(\omega T) = 2* cos(\omega T/2) * e^{-j\omega T/2}$$
4回平均
$$G(\omega T) = \frac{sin(2\omega T)}{sin(\omega T/2)} * e^{-3j\omega T/2}$$
8回平均
$$G(\omega T) = \frac{sin(4\omega T)}{sin(\omega T/2)} * e^{-7j\omega T/2}$$
10 回平均
$$G(\omega T) = \frac{sin(5\omega T)}{sin(\omega T/2)} * e^{-9j\omega T/2}$$
一般の形のn回平均もわかるよね!
■参考
・2回移動平均のオイラーの公式を使った変形については、こちらを参照
あわせて読みたい
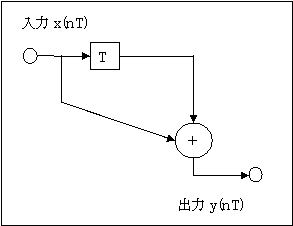

【FIRフィルタ】第1回:単純移動平均周波数特性(2回平均)
仕事で、移動平均の周波数特性の検討書を作ることになったので、昔勉強した本を引っ張りだして、書いている。「移動平均」は、株価の分析にも出てくる。ここでは、ディ...
・4回移動平均のオイラーの公式を使った変形については、こちらを参照
あわせて読みたい
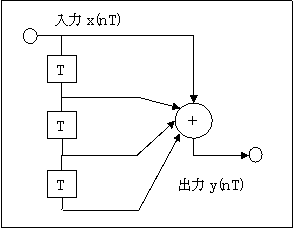

【FIRフィルタ】第5回:単純移動平均周波数特性(4回平均)
次は、4回の単純移動平均をしてみよう。 ■図の入出力関係は $$y(nT) = x(nT) + x((n-1)T) + x((n-2)T) + x((n-3)T) (式1)$$ ■伝達関数を求める。(式1)の両辺...