さて、FIRフィルタの次は、IIRフィルタを設計してみる。
FIRフィルタに関しては【FIRフィルタ】シリーズに詳しく書いてあります。
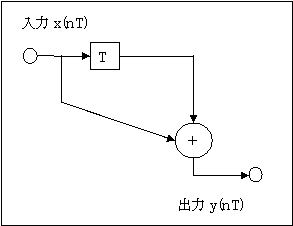
例えば、IIRフィルタの入力に1サンプリングだけ1、その次からずっと0を入力した場合、IIRフィルタ出力は小さな値になっていくが無限に続く。その波形を示す。一次遅れの例である。
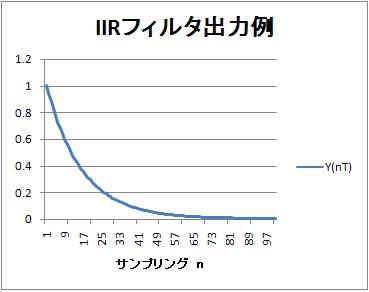
これがIIR(無限のインパルス応答)なる名前のゆえん。
さて、IIRフィルタ設計法にもいろいろあるが、わかりやすい「インパルス不変法」で一次遅れフィルタを設計してみる。
アナログフィルタ入力に細いパルスを入れた場合のアナログフィルタ出力と上記のように、最初のみ1で、次からずっと0のデータを入力したIIRフィルタ出力波形とを一致させようという方法である。
例えば、アナログフィルタが一次遅れでその入力に細いパルスを入れた時の出力が上記波形のように、指数関数的で減少し、その時定数が$\tau$[s]であるとすれば、出力波形は以下の式になる。
$$g(t) = e^{-\frac{t}{\tau}} ( t\ge 0 ) (式1)$$
この波形を T[s] ごと、サンプリングした場合、$g(t)$ の値は、上式に$t=0, t=T, t=2T, t=3T,,,$を代入して、その値は
$$1、e^{-\frac{T}{\tau}}、 e^{-\frac{2T}{\tau}}、 e^{-\frac{3T}{\tau}} 、、、$$
と変化していく。一般には
$$g(nT) = e^{-\frac{nT}{\tau}} (n=0,1,2,,,) (式2)$$
と表現できる。(式2)のz変換する。右辺は、1サンプリング遅れるごとにその値に $z^{-1} $をかけて、その総和を求める。数列のz変換は級数になる。左辺は単純に$G(z)$とおく。
$$G(z) = 1 + e^{-\frac{T}{\tau}} * z^{-1} + e^{-\frac{2T}{\tau}} * z^{-2} + e^{-\frac{3T}{\tau}} * z^{-3} + ,,, (式3)$$
これは、公比 $e^{-\frac{T}{\tau}}* z^{-1}$ の等比級数である。(式3)の両辺に $e^{-\frac{T}{\tau}} * z^{-1} $をかける。
$$G(z) * e^{-\frac{T}{\tau}}* z^{-1} = e^{-\frac{T}{\tau}} * z^{-1} + e^{-\frac{2T}{\tau}} * z^{-2} + e^{-\frac{3T}{\tau}} * z^{-3} + ,,, (式4)$$
(式3)の両辺から(式4)の両辺を引くと
$$G(z) – G(z) * e^{-\frac{T}{\tau}} * z^{-1} = 1$$
$G(z)$ について整理すると、
$$G(z) = \frac{1}{1 – e^{-\frac{T}{\tau}} * z^{-1}} (式5)$$
これが、時定数 $\tau$ の一次遅れになるIIRフィルタである。
ここで、$G(z) = Y(z) / X(z)$ を代入して、フィルタ入力$X(z)$とフィルタ出力$Y(z)$の関係式に変形する。
$$\frac{Y(z)}{X(z)} = \frac{1}{1 – e^{-\frac{T}{\tau}} * z^{-1}} (式6)$$
これを$Y(z)=$ の形に変形すると、
$$Y(z) = X(z) + e^{-\frac{T}{\tau}} * Y(z) * z^{-1} (式7)$$
これを逆z変換して、実時間の式へ戻す。$Y(z) => y(nT) , X(z) => x(nT) , Y(z)*z^{-1} => y((n-1)T)$と代入して、
$$y(nT) = x(nT) + e^{-\frac{T}{\tau}} * y((n-1)T) (式8)$$
この計算式で一次遅れのIIRフィルタができる。ブロック図は、
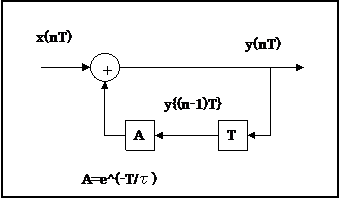
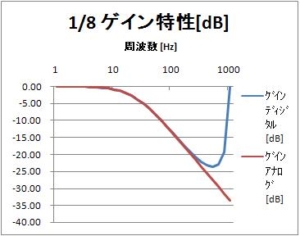
としては簡単だが、Aの値が1と 0.9 の間の値になる。実際に、T = 1 ms として、時定数$\tau=10$msとすると、$e^{-0.1}=0.904837$ となる。これを浮動小数点演算ユニット(FPU)や乗算器(かけ算を行うハードウェア)がない安い16ビットマイコンや32ビットマイコン、あるいはディジタル回路用ハードウェア記述言語のVHDLやverilogでどのように実装したらよいのか、工夫が必要。工夫については、次の記事で。