さて、今回は、インパルス不変法で設計した一次のIIRローパスフィルタの周波数特性計算式を導きます。
ディジタルフィルタの計算式は、こちらの記事

から、
$$y(nT) = x(nT) – (1-e^{-\frac{T}{\tau}}) * y((n-1)T) + y((n-1)T) (式9)$$
である。
この式において、サンプリング周期T=1ms、時定数 $\tau$ を約15msとおいて、各種の入力波形に対して、出力波形を計算した。
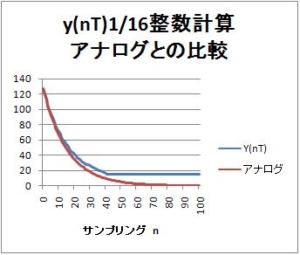
インパルス入力に対する出力波形は、
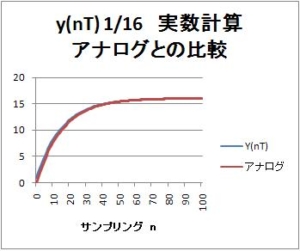
ステップ入力に対する出力波形は、
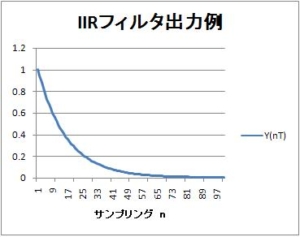
正弦波入力に対する出力波形は、

という計算してきた。
さて、(式9)の伝達関数は、こちらの【IIRフィルタ】第1回目の記事
から
$$G(z) = \frac{1}{1 – e^{-\frac{T}{\tau}} * z^{-1}} (式5)$$
この式において、$z=e^{j\omega T}$、あるいは 、$z^{-1}=e^{-j\omega T}$を代入すると、$\omega T$に関わる式
$$G(e^{j\omega T}) = \frac{1}{1 – e^{-\frac{T}{\tau}} * e^{-j\omega T}} (式10)$$
が得られる。オイラーの公式
$$e^{-j\theta} = cos\theta – j * sin\theta (式11)$$
より、
$$e^{-j\omega} = cos(\omega T) – j * sin(\omega T)$$
であるから、
$$e^{-j\omega T} = \frac{1}{1 – A * (cos(\omega T) – j * sin(\omega T))} (式12)$$
ここで、
$$A = e^{-\frac{T}{\tau}} (式13)$$
と置いた。さらに、分母の実数部と虚数部(jの付いている項)を分けて
$$G(e^{j\omega T}) = \frac{1}{1 – A * cos(\omega T) + j * A * sin(\omega T)} (式14)$$
となる。分母の
$$実数部 + j 虚数$$
の形を
$$絶対値 * e^{j位相}$$
の形に直す。この形を
$$Abs * e^{j * Angle}$$
と置けば
$$Abs = \sqrt{実数部^{2} + 虚数部^{2}}$$
$$Angle = \arctan(\frac{虚数部}{実数部}) \text{[rad]}$$
で得られる。(式14)の分母は
$$実数部 = 1 – A * cos(\omega T)$$
$$虚数部 = A * sin(\omega T)$$
なので、
$$Abs = \sqrt{(1 – Acos\omega T)^2 + (Asin\omega T)^2} (式15)$$
$$Angle = \arctan(\frac{Asin\omega T}{1 – Acos\omega T}) \text{[rad]}(式16)$$
となる。
$$\frac{1}{Abs * e^{j * Angle}} = \frac{1}{Abs} * e^{j(-Angle)}$$
なので、(式14)は、
$$G(e^{j\omega T}) = \frac{1}{Abs} * e^{j * (-Angle)} (式17)$$
となる。周波数特性のゲイン特性(振幅特性)は、(式17)の絶対値の部分から
$$g(\omega) = \frac{1}{Abs}$$
$$= \frac{1}{\sqrt{(1-Acos\omega T)^{2} + (Asin\omega T)^{2}}} (式18)$$
デシベル[dB]表示にしたいときは、
$$20 * \log | g(\omega) | \text{[dB]}$$
を計算する。
次に、位相特性は、(式17)の位相の部分から
$$\phi(\omega) = -Angle$$
$$= -\arctan{\frac{Asin\omega T}{1 – Acos\omega T}} \text{[rad]}(式19)$$
度[deg]の表示にしたいときは
$$\frac{\phi(\omega)}{2\pi} * 230 \text{[deg]}$$
を計算する。
ただし、
$$A = e^{-\frac{T}{\tau}} (式13)$$
次の記事では、周波数特性(ゲイン特性、位相特性)を計算してみよう。